The fascinating but terse 2017 paper on Machine Translation “Attention Is All You Need”, by Vaswani et al, has generated a lot of interest – and plenty of head-scratching to digest it! As far as I can tell, the Attention Function, with its Key, Value and Query inputs, is one of the obstacles in wrapping one's head around the Deep-Learning "Transformer" architecture presented in that paper.
In brief: whereas an RNN (Recursive Neural Network) processes inputs sequentially, and uses each one to update an internal state, the Transformer architecture takes in all inputs at once, and makes extensive use of “Key/Value/Query memory spaces” (called “Multi-Head Attention” in the paper.) Advantages include faster speed, and overcoming the problem of “remembering early inputs” that affects RNN’s.
That Attention Function, and related concepts, is what I will address in this blog entry. I will NOT discuss anything else about the Transformer architecture... but at the very end I'm including a few links to references and tutorials that I found helpful.
The “Attention Function” in Machine Learning is often presented as just an indexing scheme into a memory of values, as exemplified by the following annotated sketch, adapted from a talk on “Attention Is All You Need” (link).
However,
Generalizing one notch, let the range of the function now be the set of Real numbers:
Let’s now further generalize by changing the domain of the function, from the set of Natural numbers to the set of Reals:
Our limited knowledge of the function is in the form of a set of values at some points in the domain.
If we want to estimate the function value at some other point, we can interpolate; for example, using two nearby points (local interpolation), or using all available points (global interpolation.)
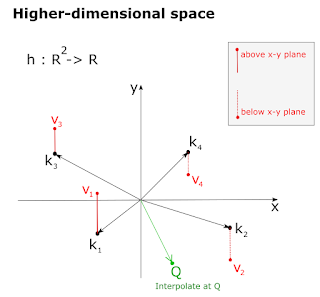
One final generalization: expand the domain of the function from R to R2.
Given a new point Q in our domain, how do we estimate the function value h(Q) ? Again, we could do local or global interpolations.
Example: hot stove. Each point represents a childhood memory. The components of K are clues to heat (such as burner color and smell); v is pain level upon touching it.
Loosely speaking, regarding the individual points as episodic memories, a person with “a lot of experience” would have many such points. A person with “wide-ranging experiences” would have points covering more of the domain (as opposed to being clustered in a small sub-region.) A person with “good intuition” would retrieve many points and make a good global interpolation.
One approach to a global interpolation function is to use a weighed average of the Values: if a particular Key is “similar” to the Query vector, use a large weight – otherwise, a small one.
One function that does just that, is: weight = 1 / (1 + dist)
(note that: dist = 0 –> weight = 1 ; dist = ∞ –> weight = 0 )
The weighed average then becomes:
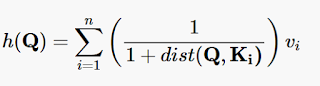[Formula 1]
Note that if Q = Kj for some j, then dist(Q , Kj) = 0, and therefore the contribution of the j-th term in the sum is the full vj. To be noted that the other Values still contribute (“leak in”) even when Q is equal to one of the Keys, unless the other Key vectors are infinitely far from Q.
The influence of distant points could be reduced by replacing the distance function with, for example, a square-distance function (which would also eliminates the need to compute square roots.)
More generally, an arbitrary exponential could be given to the distance function, and this exponential might be treated as a hyper-parameter of the interpolation function.
Since Q * Ki = || Q || || Ki || cos(θ) , where θ is the angle between the vectors, then
(Q * Ki ) / || Ki || 2 could be used as a measure of similarity between Q and Ki. Note that if Q = Ki , then the expression evaluates to 1.
Using this approach, the weighed-average interpolating function becomes:
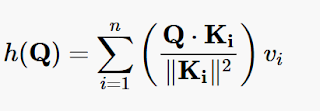[Formula 2]
Note the if all the Ki’s are orthogonal and Q = Kj for some j, then h(Q) = vj , with no “leakage” from the other Values , since all the other dot products are zero.
the Values are vectors rather than scalars.
Q is a set of queries simultaneously, packed together into a matrix; the keys and the (vector) values are also packed together into matrices K and V, respectively.
dk is the dimension of the Query and Key vectors.
EXAMPLE 1: All the Kj 's and Q are unit vectors. Use the dot-product interpolator (formula 2), repeated below:
[Formula 2, repeated]
Being unit vectors, Q * Ki = cos(α) , where α is the angle between them. Note that, even though we’re placing the vectors on the x-y plane, this is really a 1-dimentional case along the unit circle.
Using formula 2 and taking into account that all vectors are of size 1, h(Q) can be parametrized in terms of θ, where θ is the angle from the x-axis to the Q vector :
h(θ) = [Q * (1, 0)] * 15 + [Q * (0, 1)] * (-10)
= 15 cos(θ) - 10 cos(90º - θ) = 15 cos(θ) - 10 sin(θ)
Notice how, thanks to the orthogonality of the Key vectors, the original Values are attained exactly when Q is equals to a Key vector. θ = 0 corresponds to the first Key vector (1, 0), and θ = π/2 to the second one (0, 1).
Same plot in 3D – the sides of the cylinder show the interpolated values along the vertical axis:
EXAMPLE 2: let’s add a third mapping to the function of the previous example.
Then:
h(x, y) = V1*{x,y}.K1/(K1.K1) + V2*{x,y}.K2/(K2.K2) + V3*{x,y}.K3/(K3.K3)
that simplifies to:
h(x, y) = 70x/3 - 5y/3
That’s a plane in 3D space, with a big positive slant along the x-axis and a small negative slant along the y-axis:
Lacking orthogonality between the Key vectors, we no longer obtain the original values when the Query Vector equals one of the Key vectors:
EXAMPLE 3: Same data as for the previous example #2, but now using Formula 1, the one based on distances instead of dot products.
In Mathematica:
hNEWinterpolate[x_,y_] := N[V1/(1+Norm[{x,y}-K1] ) + V2/(1+Norm[{x,y}-K2] ) + V3/(1+Norm[{x,y}-K3] )]
It’s quite a different plot now, reminiscent of spacetime distortion in General Relativity. The baseline interpolated values are (asymptotically) zero, and the individual Values at the Key-vector points “distort” that baseline:
Looking at the values of this new interpolating function at the Key Vectors:
The interpolated value at the third point (K3) isn’t much affected from its original value, due to the large distance from the other points.
The range of the function could be ℜn instead of ℜ. Then, the interpolation function we’ve been looking at would create linear combinations of vectors, instead of scalars.
If h: ℜn –> ℜn , i.e. the domain and the range are the same set, then the Value vectors might be interpreted as points in the Domain – and the function h could be regarded as associating points in ℜn
Booleans (B) or other sets could take the place of ℜ. For example, the classic Pavlovian reflex could be regarded as an interpolation of h: B2 -> B (or perhaps B2 -> ℜ)
I won't discuss the actual architecture in this blog entry, except for presenting this high-level diagram, which I annotated in red to emphasize the part about Keys, Values and Queries occurring as inputs to an Attention function:
In this blog entry, I attempted to give a deeper understanding of the Attention function and the meaning of Keys, Values and Queries. The resources below go a long way to make the above diagram more intelligible:
The fascinating but terse 2017 paper on Machine Translation “In brief: whereas an RNN (Recursive Neural Network) processes inputs sequentially, and uses each one to update an internal state, the Transformer architecture takes in all inputs at once, and makes extensive use of “Key/Value/Query memory spaces” (called “Multi-Head Attention” in the paper.) Advantages include faster speed, and overcoming the problem of “remembering early inputs” that affects RNN’s.
That Attention Function, and related concepts, is what I will address in this blog entry. I will NOT discuss anything else about the Transformer architecture... but at the very end I'm including a few links to references and tutorials that I found helpful.
The “Attention Function” in Machine Learning is often presented as just an indexing scheme into a memory of values, as exemplified by the following annotated sketch, adapted from a talk on “Attention Is All You Need” (link).
 |
| (Source) |
However,
I see something deeper in it: namely, a generalization from computer memory to multi-dimensional associative memory.So, I’ll be digging deeper, trying to lay out a more mathematical foundation – and attempting to get more insight into the process, with a side foray into human cognitive processes.
A Series of Generalizations: from computer memory to multi-dimensional associative memory
A traditional computer memory can be thought of as the representation of a function from the domain of Natural numbers (the memory addresses) mapped to the set of Natural numbers (the values stored in the memory.)Generalizing one notch, let the range of the function now be the set of Real numbers:
Let’s now further generalize by changing the domain of the function, from the set of Natural numbers to the set of Reals:
Our limited knowledge of the function is in the form of a set of values at some points in the domain.
If we want to estimate the function value at some other point, we can interpolate; for example, using two nearby points (local interpolation), or using all available points (global interpolation.)
One final generalization: expand the domain of the function from R to R2.
Given a new point Q in our domain, how do we estimate the function value h(Q) ? Again, we could do local or global interpolations.
Episodic Memory
Think of all the (Ki, vi) pairs as "episodic memories".Example: hot stove. Each point represents a childhood memory. The components of K are clues to heat (such as burner color and smell); v is pain level upon touching it.
Loosely speaking, regarding the individual points as episodic memories, a person with “a lot of experience” would have many such points. A person with “wide-ranging experiences” would have points covering more of the domain (as opposed to being clustered in a small sub-region.) A person with “good intuition” would retrieve many points and make a good global interpolation.
Interpolation - Key, Value & Query
Let’s refer to:- the Ki vectors (for i = 1, …, n) as “Keys”
- the vi scalars (for i = 1, …, n) as “Values”
- the Q vector as “Query vector” (of the same dimension as the Key vectors)
- the space spanned by all the Ki vectors as “Memory Space”
One approach to a global interpolation function is to use a weighed average of the Values: if a particular Key is “similar” to the Query vector, use a large weight – otherwise, a small one.
Using Distance
For example, we could use some metric on the underlying Memory Space, such as the Euclidean distance: if dist(Q, Ki ) = 0 then use a weight of 1 for the corresponding Vi ; conversely, as the distance approaches infinity, the weight goes to 0.One function that does just that, is: weight = 1 / (1 + dist)
(note that: dist = 0 –> weight = 1 ; dist = ∞ –> weight = 0 )
The weighed average then becomes:
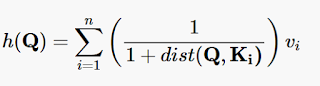[Formula 1]Note that if Q = Kj for some j, then dist(Q , Kj) = 0, and therefore the contribution of the j-th term in the sum is the full vj. To be noted that the other Values still contribute (“leak in”) even when Q is equal to one of the Keys, unless the other Key vectors are infinitely far from Q.
The influence of distant points could be reduced by replacing the distance function with, for example, a square-distance function (which would also eliminates the need to compute square roots.)
More generally, an arbitrary exponential could be given to the distance function, and this exponential might be treated as a hyper-parameter of the interpolation function.
Using Dot Products
An alternate approach is to employ the dot product of Q with the various Ki’s.Since Q * Ki = || Q || || Ki || cos(θ) , where θ is the angle between the vectors, then
(Q * Ki ) / || Ki || 2 could be used as a measure of similarity between Q and Ki. Note that if Q = Ki , then the expression evaluates to 1.
Using this approach, the weighed-average interpolating function becomes:
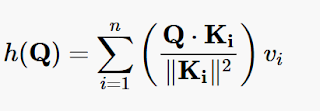[Formula 2]Note the if all the Ki’s are orthogonal and Q = Kj for some j, then h(Q) = vj , with no “leakage” from the other Values , since all the other dot products are zero.
Using SoftMax
The 2017 paper “Attention Is All You Need”, by Vaswani et al, uses the following formula:
the Values are vectors rather than scalars.
Q is a set of queries simultaneously, packed together into a matrix; the keys and the (vector) values are also packed together into matrices K and V, respectively.
dk is the dimension of the Query and Key vectors.
EXAMPLE 1: All the Kj 's and Q are unit vectors. Use the dot-product interpolator (formula 2), repeated below:
[Formula 2, repeated]Being unit vectors, Q * Ki = cos(α) , where α is the angle between them. Note that, even though we’re placing the vectors on the x-y plane, this is really a 1-dimentional case along the unit circle.
n = 2
K1 = (1, 0) , v1 = 15
K2 = (0, 1) , v2 = -10
Q unit vector.
K1 = (1, 0) , v1 = 15
K2 = (0, 1) , v2 = -10
Q unit vector.
Using formula 2 and taking into account that all vectors are of size 1, h(Q) can be parametrized in terms of θ, where θ is the angle from the x-axis to the Q vector :
h(θ) = [Q * (1, 0)] * 15 + [Q * (0, 1)] * (-10)
= 15 cos(θ) - 10 cos(90º - θ) = 15 cos(θ) - 10 sin(θ)
Notice how, thanks to the orthogonality of the Key vectors, the original Values are attained exactly when Q is equals to a Key vector. θ = 0 corresponds to the first Key vector (1, 0), and θ = π/2 to the second one (0, 1).
Same plot in 3D – the sides of the cylinder show the interpolated values along the vertical axis:
EXAMPLE 2: let’s add a third mapping to the function of the previous example.
n = 3
K1 = (1, 0) , V1 = 15
K2 = (0, 1) , V2 = -10
K3 = (-3, -3) , V3 = -50
Note that we are no longer restricting ourselves to unit vectors, nor to orthogonal Key vectors.Then:
h(x, y) = V1*{x,y}.K1/(K1.K1) + V2*{x,y}.K2/(K2.K2) + V3*{x,y}.K3/(K3.K3)
that simplifies to:
h(x, y) = 70x/3 - 5y/3
That’s a plane in 3D space, with a big positive slant along the x-axis and a small negative slant along the y-axis:
Mathematica code:
K1 = {1, 0}
K2 = {0, 1}
K3 = {-3, -3}
V1 = 15
V2 = -10
V3 = -50
hInterpolate[x_,y_]:=
N[V1*{x,y}.K1/(K1.K1)+ V2*{x,y}.K2/(K2.K2)+ V3*{x,y}.K3/(K3.K3)]
K1 = {1, 0}
K2 = {0, 1}
K3 = {-3, -3}
V1 = 15
V2 = -10
V3 = -50
hInterpolate[x_,y_]:=
N[V1*{x,y}.K1/(K1.K1)+ V2*{x,y}.K2/(K2.K2)+ V3*{x,y}.K3/(K3.K3)]
Lacking orthogonality between the Key vectors, we no longer obtain the original values when the Query Vector equals one of the Key vectors:
hInterpolate(1, 0) = 23.3333 (vs. the original 15)
hInterpolate (0, 1) = -1.66667 (vs. the original -10)
hInterpolate(-3, -3) = -65 (vs. the original -50)
hInterpolate (0, 1) = -1.66667 (vs. the original -10)
hInterpolate(-3, -3) = -65 (vs. the original -50)
EXAMPLE 3: Same data as for the previous example #2, but now using Formula 1, the one based on distances instead of dot products.
In Mathematica:
hNEWinterpolate[x_,y_] := N[V1/(1+Norm[{x,y}-K1] ) + V2/(1+Norm[{x,y}-K2] ) + V3/(1+Norm[{x,y}-K3] )]
It’s quite a different plot now, reminiscent of spacetime distortion in General Relativity. The baseline interpolated values are (asymptotically) zero, and the individual Values at the Key-vector points “distort” that baseline:
Looking at the values of this new interpolating function at the Key Vectors:
hNEWinterpolate(0, 1) = 2.52453 (vs. the original 15)
hNEWinterpolate(1, 0) = -12.1201 (vs. the original -10)
hNEWinterpolate(-3, -3) = -49.1667 (vs. the original -50)
hNEWinterpolate(1, 0) = -12.1201 (vs. the original -10)
hNEWinterpolate(-3, -3) = -49.1667 (vs. the original -50)
The interpolated value at the third point (K3) isn’t much affected from its original value, due to the large distance from the other points.
Generalizations: different Domains and Ranges of the Memory Function
In the previous examples, the memory function was h: ℜ2 –> ℜThe range of the function could be ℜn instead of ℜ. Then, the interpolation function we’ve been looking at would create linear combinations of vectors, instead of scalars.
If h: ℜn –> ℜn , i.e. the domain and the range are the same set, then the Value vectors might be interpreted as points in the Domain – and the function h could be regarded as associating points in ℜn
Booleans (B) or other sets could take the place of ℜ. For example, the classic Pavlovian reflex could be regarded as an interpolation of h: B2 -> B (or perhaps B2 -> ℜ)
Helpful Resources on the Deep-Learning "Transformer" Architecture
As promised in the opening sentences, below is a listing of resources (mainly blogs and videos) that I found helpful when I first encountered the Deep-Learning "Transformer" Architecture that was introduced in the 2017 paper “Attention Is All You Need”.I won't discuss the actual architecture in this blog entry, except for presenting this high-level diagram, which I annotated in red to emphasize the part about Keys, Values and Queries occurring as inputs to an Attention function:
In this blog entry, I attempted to give a deeper understanding of the Attention function and the meaning of Keys, Values and Queries. The resources below go a long way to make the above diagram more intelligible:
| URL | title | comments |
|---|---|---|
| http://jalammar.github.io/illustrated-transformer/ | The Illustrated Transformer – Jay Alammar – Visualizing machine learning one concept at a time | Extremely helpful! Blog on which the helpful video https://www.youtube.com/watch?v=S0KakHcj_rs (next entry) is based |
| https://www.youtube.com/watch?v=S0KakHcj_rs | [Transformer] Attention Is All You Need | AISC Foundational - YouTube | Very helpful and well-presented. Based on the blog http://jalammar.github.io/illustrated-transformer/ (previous entry) |
| https://distill.pub/2016/augmented-rnns/ | Attention and Augmented Recurrent Neural Networks | very readable and helpful |
| https://www.youtube.com/watch?v=iDulhoQ2pro | Attention Is All You Need - YouTube | quite helpful - but it glosses over the later part. It feels like a "part 1" in need of a "part 2" |
| https://www.youtube.com/watch?v=W2rWgXJBZhU | Attention in Neural Networks - YouTube | helpful |
| https://jalammar.github.io/visualizing-neural-machine-translation-mechanics-of-seq2seq-models-with-attention/ | Visualizing A Neural Machine Translation Model (Mechanics of Seq2seq Models With Attention) – Jay Alammar – Visualizing machine learning one concept at a time | Helpful animations for RNN translation, without and with Attention. However, it glosses over a few things |
| http://mlexplained.com/2017/12/29/attention-is-all-you-need-explained/ | Paper Dissected: "Attention is All You Need" Explained | Machine Learning Explained | clear language. Helpful |
| https://medium.com/syncedreview/a-brief-overview-of-attention-mechanism-13c578ba9129 | A Brief Overview of Attention Mechanism – SyncedReview – Medium | insightful but with tortured English, errors and omissions |
| https://medium.com/@adityathiruvengadam/transformer-architecture-attention-is-all-you-need-aeccd9f50d09 | Transformer Architecture: Attention Is All You Need | some clarifications - though also plenty of rehashing - of the terse "Attention is All You Need" paper. Nearly unreadable. One intriguing (but unclear) animation |
| https://medium.com/inside-machine-learning/what-is-a-transformer-d07dd1fbec04 | What is a Transformer? – Inside Machine learning – Medium | Some clarifications - but mostly rehashing - of the terse "Attention is All You Need" paper |
| https://ai.googleblog.com/2017/08/transformer-novel-neural-network.html | Transformer: A Novel Neural Network Architecture for Language Understanding | 2017. Brief. One intriguing (but unclear) animation |
| https://www.youtube.com/watch?v=rBCqOTEfxvg | Attention is all you need attentional neural network models – Łukasz Kaiser - YouTube | Directly from a Google guy... but on the confusing side |
| https://www.youtube.com/watch?v=SysgYptB198 | C5W3L07 Attention Model Intuition (Part 7 of a series) | helpful |
| https://www.youtube.com/watch?v=quoGRI-1l0A | C5W3L08 Attention Model (Part 8 of a series) | helpful - details from part 7 |
Comments
Post a Comment